Teorema del binomio
En matemáticas, el teorema del binomio es un resultado que proporciona el desarrollo de la potencia de una suma. Este teorema establece:
|
donde  recibe el nombre de coeficiente binomial y representa el número de formas de escoger k elementos a partir de un conjunto con n elementos. Usualmente el teorema del binomio se expresa en la siguiente variante:
recibe el nombre de coeficiente binomial y representa el número de formas de escoger k elementos a partir de un conjunto con n elementos. Usualmente el teorema del binomio se expresa en la siguiente variante:
| |
Usando la fórmula para calcular el valor de  (que también es representado ocasionalmente como C(n,k) o
(que también es representado ocasionalmente como C(n,k) o 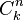 ) se obtiene una tercera representación:
) se obtiene una tercera representación:
| |
Como ejemplo, para n=2, n=3, n=4:
Para obtener la expansión de las potencias de una resta, basta con tomar -y en lugar de y en el caso anterior. La expresión (2) queda de la siguiente forma:
Teorema generalizado del binomio (Newton)
Isaac Newton generalizó la fórmula para tomar otros exponentes, considerando una serie infinita:
(3)
Donde r puede ser cualquier número complejo (en particular, r puede ser cualquier número real, no necesariamente positivo ni entero), y los coeficientes están dados por:
(el k = 0 es un producto vacío y por lo tanto, igual a 1; en el caso de k = 1 es igual a r, ya que los otros factores (r − 1), etc., no aparecen en ese caso).
Una forma útil pero no obvia para la potencia recíproca:
La suma en (3) converge y la igualdad es verdadera siempre que los números reales o complejos x e y sean suficientemente cercanos, en el sentido de que el valor absoluto | x/y | sea menor a uno.
BIBLIOGRAFIA:
http://es.wikipedia.org/wiki/Teorema_del_binomio
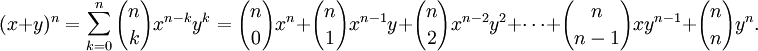
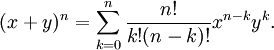
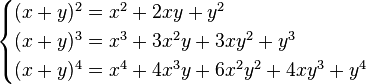
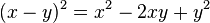
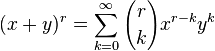
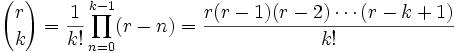

No hay comentarios:
Publicar un comentario