Sucesión matemática
Una sucesión matemática es una aplicación definida sobre los números naturales. Es costumbre representarla con las letras u, v, w... para designarlas, en vez de f, g, h... que sirven para las funciones. Del mismo modo, la variable se nota usualmente n (por natural) en vez de x, habitual para las variables reales.
Por convención, se escribe un (en vez de u(n)), la imagen de n por la sucesión u, o sea el término número n+1 de la sucesión u (el primer término es habitualmente u0).
Existen esencialmente dos maneras de definir una sucesión: explícitamente o implícitamente.
También asociado a una sucesión está el concepto de convergencia.
Definición explícita
La definición es explícita cuando se da una fórmula que permite hallar un mediante un cálculo único donde no interviene otra variable que n. En otras palabras, un es una función de n: un = f(n).
Es el caso representado por el primer gráfico, donde la función es polinomial. Los términos de la sucesión son las ordenadas de los puntos rojos, cuyas abscisas son los enteros naturales.
Cuando la función f es definida también en los reales (como en la figura), el estudio de f (límite en + ∞ variaciones, extremos) permite conocer perfectamente u:
- Si f tiende hacia l (en + ∞) entonces también lo hace u. La recíproca es errónea, como lo muestra la función f(x) = sin(2π·x), que no tiene límite mientras que un = f(n) es siempre nulo y u tiende por lo tanto hacia cero.
- Si f es creciente en un intervalo [a; b] entonces u lo es para los valores enteros positivos del intervalo (o sea sobre [a; b] ∩
 ).
). - Para los extremos, la cosa se complica: si los extremos de f no corresponden a valores enteros de x, entonces se tiene que considerar los naturales más próximos y comparar los un correspondientes. En la figura, f tiene un mínimo relativo en el intervalo ]2; 3[, y como u2 <>3, u2 es un mínimo relativo de u. El máximo relativo de f en ]6; 7[ da dos máximos relativos de u porque u6 = u7.
Sin embargo, existen métodos para estudiar u sin estudiar f: el sentido de variación se puede determinar con el signo de un+1 - un (si es positivo, u crece), o comparando la fracción un+1/un con 1 (apropiado cuando u es de signo constante, a ser posible positivo). Estos cálculos pueden ser más sencillos cuando f tiene una función derivada complicada.
En algunos casos, la función f que aparece en un = f(n) no puede extenderse a . Es el caso si definimos un como el número de factores propios de n por ejemplo, u otras funciones aritméticas, como la función fi de Euler o la Función de Möbius µ . El estudio clásico de las funciones, mediante la derivación, es entonces imposible.
Las sucesiones aritméticas
Una sucesión aritmética puede ser definida como función de n:
También puede ser definida por inducción de la siguiente forma:
Al número real r se le denomina razón de la sucesión.
Si la razón es positiva, la sucesión crece, y tiende hacia + ∞. Si es negativa, decrece y tiende hacia - ∞. Si es nula, la sucesión es constante.
Existe una fórmula muy sencilla para sumar números en progresión aritmética (es decir términos sucesivos de una sucesión aritmética): se multiplica el término medio, que es el promedio de los términos extremos, por el número de términos. Esta fórmula toma las formas siguientes, según el contexto:
 |
 |
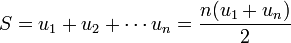 |
Como caso particular muy frecuente: 
A veces lo más difícil es encontrar el número de términos para poder aplicar la fórmula. Si el primer término a sumar vale a, el último vale b, y la razón es r, entonces el número de términos en la suma es:
Por ejemplo, para la suma: S = 1492 + 1499 + 1506 + ... 2003 de términos consecutivos de una sucesión de razón 7, encontramos 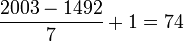 términos, y la suma es
términos, y la suma es 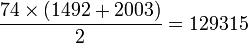 .
.
Las sucesiones geométricas
Una sucesión geométrica puede ser definida como función de n:
También puede ser definida por inducción de la siguiente forma:
Al número real r se le denomina también razón de la sucesión. A menudo se la denota q.
El comportamiento de la sucesión geométrica depende del signo del primer término y del valor de su razón.
Si la razón es positiva, entonces la sucesión es monótona, y tiene un aspecto muy regular, que se puede prolongar por una función de tipo exponencial de base r:  se prolonga en f(x) = b·rx.
se prolonga en f(x) = b·rx.
Se distinguen cuatro casos, como se ve en la figura siguiente; las ordenadas de los puntos negros son los valores de la sucesión, y la curva representa la función:
Si la razón es negativa, entonces la sucesión es oscilante. Se distinguen dos casos en función de si r es menor que -1 ó no. El signo del primer término no modifica el aspecto general de la sucesión (cambiar de signo equivale a una simetría alrededor del eje horizontal, y aquí no se nota mucho). Las potencias rn con r negativo no se generalizan a los reales, salvo convención particular, y por lo tanto no existe una función natural que prolongue la sucesión. En la figura siguiente se ha multiplicado la función |r|x por el factor cos πx para simular el cambio periódico de signo.
Si el término inicial es nulo, o si la razón vale -1, 0 ó 1, la sucesión no entra en la clasificación anterior, pero no importa pues en tal caso carece de interés.
Descartando estos casos particulares, se puede decir que la convergencia de la sucesión depende del valor absoluto de la razón:
- si |r| > 1, no converge, y si |r| <>
Notemos q la razón, y supongamos q ≠ 1. Entonces la suma de números en progresión geométrica es dada por la fórmula siguiente, bajo tres formas equivalentes:
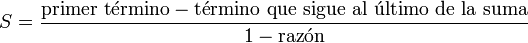 |
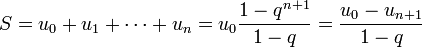 |
 |
Fórmulas
Suponiendo que An sea el término cualquiera, Ak el término que ocupa la posición "k", y A1 el primer término de la sucesión:
Para hallar un término cualquiera en una sucesión geométrica, se debe usar: 
Para sumar los "n" primeros términos de una sucesión geométrica: 
Para sumar todos los números de una sucesión (Suma infinita):  . Esta fórmula sólo es aplicable cuando
. Esta fórmula sólo es aplicable cuando
Para calcular el producto de los nº primeros términos de una sucesión: 
BIBLIOGRAFIA:
http://es.wikipedia.org/wiki/Sucesi%C3%B3n_matem%C3%A1tica



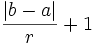

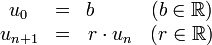
No hay comentarios:
Publicar un comentario