miércoles, 7 de octubre de 2009

NUMEROS COMPLEJOS

Número complejo

El término número complejo describe la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i). Los números complejos se utilizan en todos los campos de las matemáticas, en muchos de la física (y notoriamente en la mecánica cuántica) y en ingeniería, especialmente en la electrónica y las telecomunicaciones, por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica.
En matemáticas, los números constituyen un cuerpo y, en general, se consideran como puntos del plano: el plano complejo. La propiedad más importante que caracteriza a los números complejos es el teorema fundamental del álgebra, que afirma que cualquier ecuación algebraica de grado n tiene exactamente n soluciones complejas.

Los números complejos son una extensión de los números reales, cumpliéndose que . Los números complejos representan todas las raíces de los polinomios, a diferencia de los reales.

Los números complejos son la herramienta de trabajo del álgebra ordinaria, llamada álgebra de los números complejos, así como de ramas de las matemáticas puras y aplicadas como variable compleja, aerodinámica y electromagnetismo entre otras de gran importancia.

Contienen a los números reales y los imaginarios puros y constituyen una de las construcciones teóricas más importantes de la inteligencia humana. Los análogos del cálculo diferencial e integral con números complejos reciben el nombre de variable compleja o análisis complejo.

\begin{array}{ll} \mathbb{C} & \mbox{Complejos} \begin{cases} \mathbb{R} & \mbox{Reales} \begin{cases} \mathbb{Q} & \mbox{Racionales} \begin{cases} \mathbb{Z} & \mbox{Enteros} \begin{cases} \mathbb{N} & \mbox{Naturales} \\ & \mbox{Cero} \\ & \mbox{Enteros negativos} \end{cases}\\ & \mbox{Fraccionarios} \end{cases}\\ & \mbox{Irracionales} \end{cases}\\ & \mbox{Imaginarios} \end{cases} \end{array}

Definición


Definiremos cada complejo z como un par ordenado de números reales (a, b) ó (Re(z), Im(z)), en el que se definen las siguientes operaciones:

  • Suma
(a, b) + (c, d) = (a+c) +\; (b+d)i
  • Multiplicación
(a, b) \cdot (c, d) = (ac - bd) +\; (ad + cb)i
  • Igualdad
(a, b) = (c, d) \iff a = c \and b = d

Al primer componente (que llamaremos a) se la llama parte real y al segundo (que llamaremos b), parte imaginaria. Se denomina número imaginario puro a aquel que esta compuesto sólo por la parte imaginaria, es decir, aquel en el que a = 0 .

Los números complejos forman un cuerpo, el cuerpo complejo, denotado por C (o más apropiadamente por el carácter unicode ℂ ). Si identificamos el número real a con el complejo (a, 0), el cuerpo de los números reales R aparece como un subcuerpo de C. Más aún, C forma un espacio vectorial de dimensión 2 sobre los reales. Los complejos no pueden ser ordenados como, por ejemplo, los números reales: C no puede ser convertido de ninguna manera en un cuerpo ordenado.

La multiplicación de números complejos es asociativa, conmutativa y distributiva:

Sean z,w,s \in \mbox{C}


I) (zw)s = z(ws)\,

II) zw = wz\,

III) z(w + s) = zw + zs \,


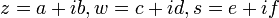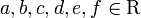
Sean z = a + i b, w = c + i d, s = e + i f \, con a,b,c,d,e,f \in \mbox{R}


Por demostrar la propiedad asociativa (I)

(zw)s = [(a + i b)(c + i d)](e + i f) = [(ac - bd) + i (bc + ad)](e + i f)\,


[e(ac - bd) - f(bc + ad)] + i [e(bc + ad) + f(ac - bd) = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,


Por otra parte

z(ws) = (a + i b)[(c + i d)(e + i f)] = (a + i b)[(ce - df) + i (de + cf)]\,


[a(ce - df) - b(de + cf)] + i [b(ce - df) + a(de + cf)] = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,

Entonces se cumple (zw)s = z(ws)\,.

Unidad imaginaria


Tomando en cuenta que (a, 0) \cdot (0, 1) = (0, a), se define un número especial en matemáticas de gran importancia, el número i o unidad imaginaria, definido como

\mathrm{i} = (0, 1) \,\!

De donde se deduce inmediatamente que,

\mathrm{i}^2 = \mathrm{i} \cdot \mathrm{i} = (0, 1) \cdot (0, 1) = (-1, 0) = -1

Representación binomial


Un número complejo se representa en forma binomial como:

z = a + bi \,

La parte real del número complejo y la parte imaginaria, se pueden expresar de varias maneras, como se muestra a continuación:

a = \hbox{Re}(z)=\Re(z)
b = \hbox{Im}(z)=\Im(z)

Plano de los números complejos o Diagrama de Argand


El concepto de plano complejo permite interpretar geométricamente los números complejos. La suma de números complejos se puede relacionar con la suma con vectores, y la multiplicación de números complejos puede expresarse simplemente usando coordenadas polares, donde la magnitud del producto es el producto de las magnitudes de los términos, y el ángulo contado desde el eje real del producto es la suma de los ángulos de los términos. Los diagramas de Argand se usan frecuentemente para mostrar las posiciones de los polos y los ceros de una función en el plano complejo. El análisis complejo, la teoría de las funciones complejas, es una de las áreas más ricas de la matemática, que encuentra aplicación en muchas otras áreas de la matemática así como en física, electrónica y muchos otros campos.

Valor absoluto o módulo, conjugado y distancia


Valor absoluto o módulo de un número complejo

El valor absoluto, módulo o magnitud de un número complejo z viene dado por la siguiente expresión:

|z| = \sqrt{\hbox{Re}^2(z) + \hbox{Im}^2(z)}

Si pensamos en z como algún punto en el plano; podemos ver, por el teorema de Pitágoras, que el valor absoluto de un número complejo coincide con la distancia euclídea desde el origen del plano.

Si el complejo está escrito en forma exponencial z = r eiφ, entonces |z| = r. Se puede expresar en forma polar como z = r (cosφ + isenφ), donde cosφ + isenφ = eiφ es la conocida fórmula de Euler.

Podemos comprobar con facilidad estas cuatro importantes propiedades del valor absoluto

\left| z \right| = 0 \Longleftrightarrow z = 0
\left| z + w \right| \leq |z| + |w|
\left| zw \right| = |z||w|
\left| z - w \right| \ge |z| - |w|

para cualquier complejo z y w.

Por definición, la función distancia queda como sigue d(z, w) = |z - w| y nos provee de un espacio métrico con los complejos gracias al que se puede hablar de límites y continuidad. La suma, la resta, la multiplicación y la división de complejos son operaciones continuas. Si no se dice lo contrario, se asume que ésta es la métrica usada en los números complejos.

Conjugado de un número complejo


Dos binomios se llaman conjugados si solo difieren en su signo central, por ejemplo, los dos binomios: 3m - 1 y 3m + 1 son conjugados.

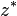El conjugado de un complejo z (denotado como \bar{z} ó z^* \,\!) es un nuevo número complejo, definido así:

\bar{z} = a - \mathrm{i}b \Longleftrightarrow z = a + \mathrm{i}b

Se observa que ambos difieren en el signo de la parte imaginaria.

Con este número se cumplen las propiedades:

\overline{z + w} = \bar{z} + \bar{w}
z+\overline{z} = 2\cdot \hbox{Re}(z)
z-\overline{z} = 2i\cdot \hbox{Im}(z)
\overline{zw} = \bar{z} \bar{w}
z \in \mathbb{R} \Longleftrightarrow \bar{z} = z
|z|^2 = z\bar{z}
z \neq 0 \Longrightarrow \frac{1}{z} = \frac{\bar{z}}{|z|^2}

Esta última fórmula es el método elegido para calcular el inverso de un número complejo si viene dado en coordenadas rectangulares.

Representación trigonométrica (polar) y representación geométrica


Algunas veces, la representación de números complejos en la forma z = a + i b (coordenadas ortogonales) es menos conveniente que otra representación, usando coordenadas polares.

Representamos el número complejo z en el plano de números complejos como un punto con coordenadas (a, b), denominado vector de posición.

Trazamos la distancia desde el punto (0,0) hasta (a, b), a la que llamaremos r, y, que como se ha visto antes, es igual al módulo de z, expresado | z | .

Esta distancia forma, con respecto al eje real positivo, un ángulo, denominado \phi \,.

La representación polar nos permite expresar este número complejo en función de r y del ángulo \phi \,:

z = r e^{\mathrm{i}(\phi + 2\pi{}k) \,}

Despejamos a y b en las expresiones anteriores y, utilizando la representación binomial:

z = a + \mathrm{i}b ;\; z = r\cos{\phi} + \mathrm{i}r\sin{\phi}

Sacamos factor común r:

z = r \left( \cos{\phi} + \mathrm{i}\sin{\phi} \right)

Frecuentemente, esta expresión se abrevia convenientemente de la siguiente manera:

\ z = r \; \operatorname{cis} \; {\phi}

la cual solo contiene las abreviaturas de las razones trigonométricas coseno, la unidad imaginaria y la razón seno del argumento respectivamente.

Según esta expresión, puede observarse que para definir un número complejo tanto de esta forma como con la representación binomial se requieren dos parámetros, que pueden ser parte real e imaginaria o bien módulo y argumento, respectivamente.

Según la Fórmula de Euler, vemos que:

\cos{\phi} + \mathrm{i}\sin{\phi} = e^{\mathrm{i}\phi} ;\; z = r e^{i\phi}

No obstante, el ángulo φ no está unívocamente determinado por z, como implica la fórmula de Euler:

\forall{k}{\in}\mathbb{Z}\; z = e^{\mathrm{i}(\phi + 2\pi{}k)}

Por esto, generalmente restringimos φ al intervalo [-π, π] y a éste φ restringido lo llamamos argumento principal de z y escribimos φ = Arg(z). Con este convenio, las coordenadas estarían unívocamente determinadas por z.

La multiplicación de números complejos es especialmente sencilla con la notación polar:

z_1 z_2 = rse^{\mathrm{i}(\phi + \psi)} \Leftrightarrow z_1 z_2 = r e^{\mathrm{i}\phi} s e^{\mathrm{i}\psi}

División:

\frac{z_1}{z_2} = \frac{r}{s} e^{\mathrm{i}(\phi - \psi)}

Potenciación:

z^n = r^n e^{\mathrm{i} \phi n} \Leftrightarrow z^n = \left( r e^{i\phi} \right)^{n}
z^n =(a + b\mathrm{i})^n = {n \choose 0}a^n + {n \choose 1} a^{n-1}b\mathrm{i} + {n \choose 2}a^{n-2} \left ( b \mathrm{i} \right)^2 + \ldots + {n \choose {n-1}}a \left ( b \mathrm{i} \right ) ^{n-1} + {n \choose n} \left (b\mathrm{i} \right)^n
BIBLIOGRAFIA:
http://es.wikipedia.org/wiki/N%C3%BAmero_complejo








Publicado por en

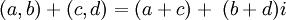
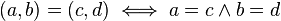
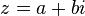
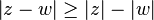
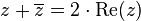
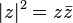
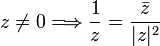
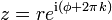
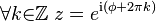
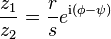
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)